点解踩蕉皮会滑倒?搞笑诺贝尔奖脑洞大开|STEM教室
2024-09-04 14:00 
每年的诺贝尔奖志在表彰在不同领域作出最重要发现或发明的人,但同一时间亦有一个「搞笑诺贝尔奖」(Ig Nobel Prize),表彰十种「不寻常、推崇想像,并激起人们对科学、医学与科技兴趣」的科学研究,例如踩蕉皮的摩擦力、怎样捧咖啡最安全等等。科研除了帮助人类解决大问题,亦可解决生活的疑难杂症。今期STEM教室就整理「搞笑诺贝尔奖」历届得奖研究,从中挑选了四项让人「脑洞大开」的物理学研究,和大家分享科学的趣味。
历届的搞笑诺贝尔奖和特制奖杯:






基本概念:力学
力学是物理世界的重要范畴,接下来提到的四项实验都与力学有关,而应用力学本身亦可以分为静力学、 动力学、运动学。静力学研究物体的平衡状态;动力学研究物体的运动状态和因素;运动学则把物体视为「刚体」,专门描述物体的运动,而不考虑作用力、质量、性质等,应用力学较常用作解决工程技术问题。

2021:街头动力学→行路勿低头
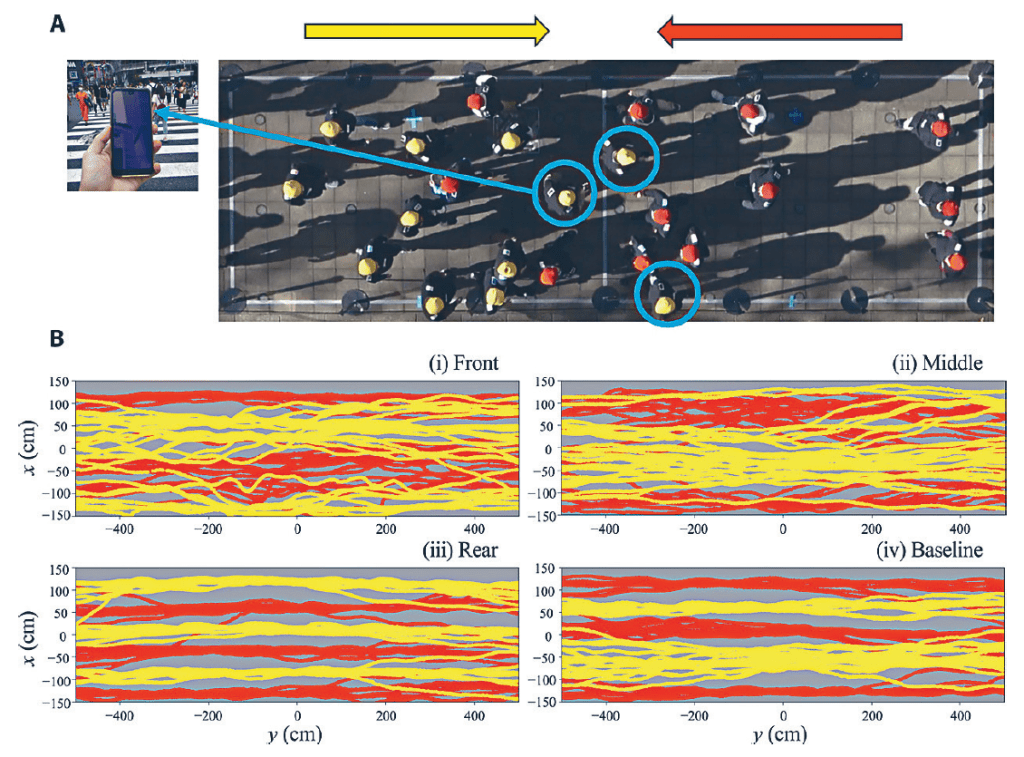
街道人来人往,为甚么我们很少迎头相撞?物理学家提出了「自我组织」(self-organization), 解释「行人自动跟随相同方向人潮」的现象。但是,自从出现了智能手机,人人成为低头族,打破了这项不明文规定。东京大学先端科学技术研究中心的村上久(Hisashi Murakami)博士邀请了五十四名大学生,分成左右两组,各二十七人。两边的人分别戴上黄色和红色的帽,以正常的走路速度朝另一边前进,研究者以摄影自动追踪系统,记录和研究他们的行进速度、分布、转弯角度等数据,改变不同变项,最后得出研究结果。
他发现只要路人队伍的「领头羊」滑手机,紧随其后的路人便很容易「方寸大乱」,造成大挤塞的情况;相反,若是队伍的中间或后面的路人滑手机,对行人路秩序产生的影响则少得多。
有兴趣了解研究过程的同学点击这里阅读完整论文。
2017:流体动力学→倒着捧咖啡
同学有没有试过「倒泻」饮品? 如果有,便要学学二○一七年「搞笑诺贝尔奖」得主Han-Ji-Won,他还在韩国读高中的时候,就以十五页论文研究得出「最强」捧咖啡方法:「抓住杯口,向前看,倒着走。」

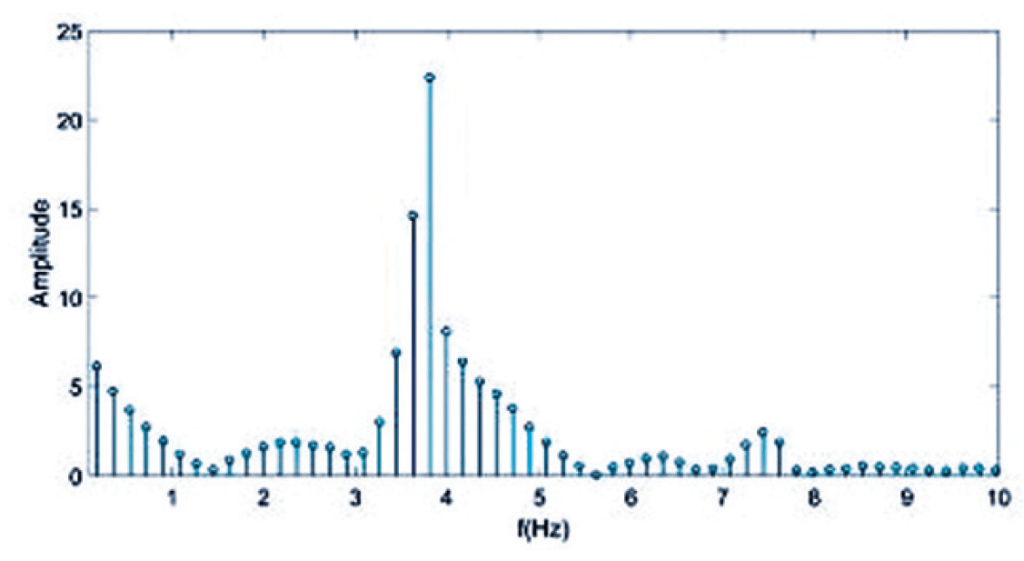
看来令人哭笑不得的研究题目,自然少不了实际的科学知识和严谨的研究方法。这名「无聊」的韩国高中生观察一般人捧咖啡杯的情况,发现杯内液体的晃动可分成前后、左右、上下几种模式,而不同模式之间晃动的频率并不一致,当晃动叠合,杯内液体便会调皮地溢出;加上不同形状的杯子亦会影响液体的晃动模式。


至此,我们已得出几个影响液体溢出的变量,那么要如何找出最不容易令液体溢出的方法呢?
手机APP记录移动数据
原来这个实验十分简单,只要你有一部智能手机,下载能够记录手机移动数据的应用程式(Sensor Logger),打开程式后把手机盖在杯子上,模拟不同的行走方法,程式会记录手机前后、左右、上下的方位改变、速度,甚至磁场改变,分析这些数据,例如频率和振幅,找出最理想的捧杯方式。

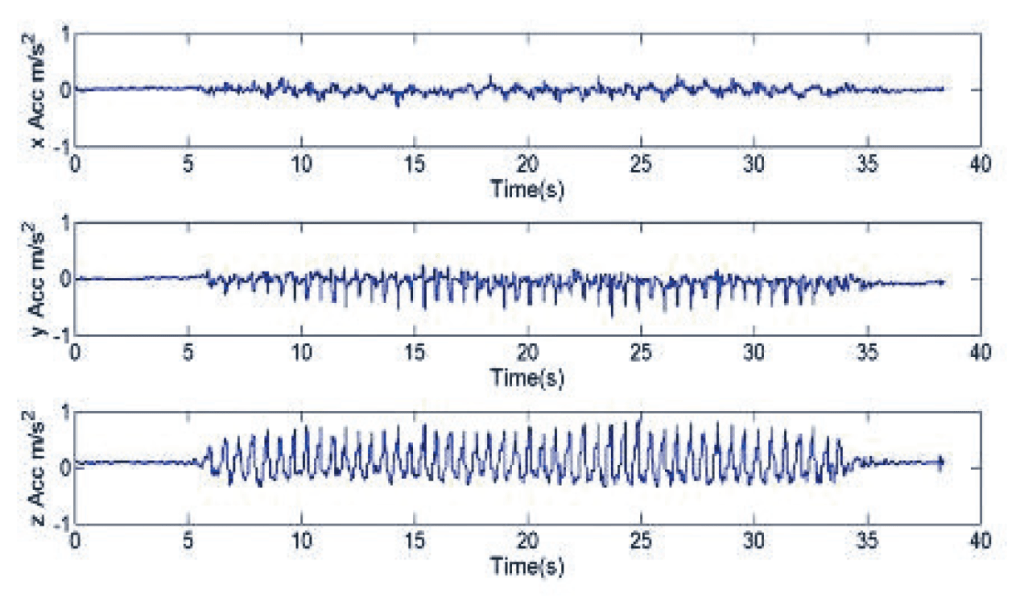
充满好奇心的同学,不难想像在日常生活中,也可以利用这个应用程式来研究身边大小事,例如「哪一条巴士綫路最适合睡觉」、「如何跑步最省力」等等,只要多观察,科学实验原来也可以很简单。
Sensor Logger App
有兴趣了解研究过程的同学点击这里阅读完整论文。
2014:香蕉摩擦力→滑倒的真相
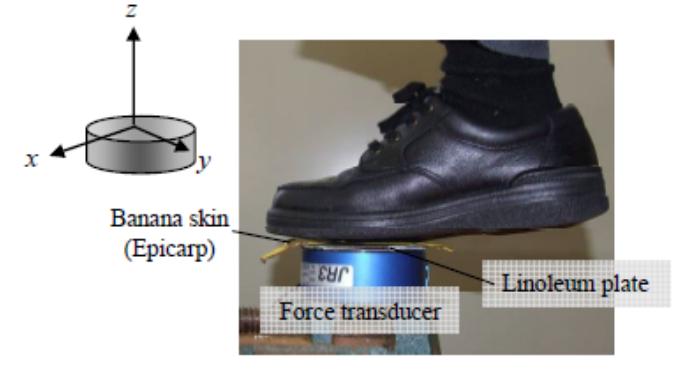
踩蕉皮滑倒的画面常令人捧腹大笑,是电影中常见的桥段,不知道各位同学有没有踩蕉皮的经验呢?日本北里大学的研究团队决定认真研究「香蕉皮有多滑」,找出蕉皮令人滑倒的真相,这项看似开玩笑的科学研究,夺得二○一四年「搞笑诺贝尔奖」。

这个「搞笑」的实验用上可以测量正向力和横向力的感知器,在感知器上放一块地板,地板上放置黄皮朝上的香蕉皮,然后「不幸」的研究人员穿鞋子踩上去一滑,将结 果得出的横向力除以正向力(μ =(fx2+fy2)0.5/fz),可得出蕉皮与地板之间的摩擦系数。多次测试后,研究团队的得出蕉皮的摩擦系数是0.07。研究又引用其他科学文献指出,对一般人的行路模式而言,脚踏在摩擦系数低于0.1的表面,滑倒机率大于百分之九十。
有兴趣了解研究过程的同学点击这里阅读完整论文。
补充资料
摩擦系数(Friction)
摩擦系数是两个物体表面之间,摩擦力与正向压力的比值,受滑动面的性质、粗糙度、表面状态影响,数值愈大,代表物件表面愈粗糙。下表是一 些常见物件之间的摩擦系数。
| 物件一 | 物件二 | 表面状态 | (静)摩擦系数(μ) |
| 冰 | 冰 | 清洁 | 0.1 |
| 木材 | 木材 | 乾燥 | 0.4 |
| 皮革 | 橡胶 | 乾燥 | 0.61 |
| 汽车胎 | 沥青 | 乾燥 | 0.72 |
1996:牛油面着地→面包力学图
来自国外的都市传闻,面包总是以涂有牛油的一面着地 (Bread always falls on the buttered side down),最初来自诗人的讽刺,透露对日常中「微不幸」的无奈。英国物理学家罗伯特.马修斯(Robert Matthews)是墨菲定律(Murphy's law)的研究学者,他非常严肃地面对这个问题,决定用科学方法去验证这个都市传闻,设计面包坠地的力学图(见图六),数学计算牛油面向地板的概率,写成论文〈掉落的吐司、墨菲法则和基本常数〉发表于《欧洲物理学期刊》,勇夺一九九六年的「搞笑诺贝尔奖」。

经过几页纸的数学计算,罗伯特的结论只是,「从早餐桌上掉下的吐司会以牛油的一面着地,是宇宙中必然会发生的。」但因为数学模型的限制,无法完全考虑现实的各种影响因素,罗伯特其后以实验方式,统计一千次面包掉在地板的结果,在9,821次有效掉落结果,其中6,101次以牛油一面落地,概率达到62%,超出常理50%的预测结果,某程度支持了这项都市传闻。
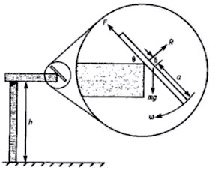
有兴趣了解研究过程的同学点击这里阅读完整论文。
补充资料
墨菲定律(Murphy's law)
墨菲定律指「有可能出错的事总会出错」,大多时候会从心理学的角度去解释,但其实亦可以数学式表达:
设出错的概率为E、重复做一件事的次数为n,那么不出错的概率可以1 - E(全部可能-出错的可能=不出错的可能)表示,而连续n次不出错的概率为(1 - E)^n。
试考虑一下,不能连续n次不出错的概率(即在n次中,至少出错1次的概率)便可得出数学式:
P(possibility)= 1 -(1 - E)^n
因为0<1 - E<1,所以当n愈大(重复次数愈多),(1 - E)^n愈接近0,即P愈接近1(「1」在概率上代表必然发生)。
结论是,只要重复做一件事情的次数足够多,便一定会发生错误;也许各位同学下次做错题目,可以用墨菲定律跟老师解释是因为功课太多了。
文:卢家彦、星岛中学学生报《S-FILE》编辑部;图:网上图片

最新回应