點解踩蕉皮會滑倒？搞笑諾貝爾獎腦洞大開｜STEM教室

每年的諾貝爾獎志在表彰在不同領域作出最重要發現或發明的人，但同一時間亦有一個「搞笑諾貝爾獎」（Ig Nobel Prize），表彰十種「不尋常、推崇想像，並激起人們對科學、醫學與科技興趣」的科學研究，例如踩蕉皮的摩擦力、怎樣捧咖啡最安全等等。科研除了幫助人類解決大問題，亦可解決生活的疑難雜症。今期STEM教室就整理「搞笑諾貝爾獎」歷屆得獎研究，從中挑選了四項讓人「腦洞大開」的物理學研究，和大家分享科學的趣味。

歷屆的搞笑諾貝爾獎和特製獎杯：

2019年頒獎主題為「習慣」，特製的「習慣獎盃」上聚集了讓人上癮的元素：外帶咖啡杯、口香糖、彩券、手機、牙刷、煙等，另外還有一張紙製獎狀，以及「十兆」元辛巴威幣獎金。

2017年的主題為「不確定性(Uncertainty)」，圖為法國研究員法丹（Marc-Antoine Fardin）因「一隻貓可以同時是固體和液體嗎？」的研究報告得獎而上台領獎的一刻。

台灣裔美國籍科學家胡立德以「哺乳動物尿尿時間為21秒」研究得獎2015年搞笑諾貝爾物理學獎。

2014年得獎研究包括人踩到香蕉皮不會馬上滑倒、狗大便時呈南北向姿勢等。圖為搞笑諾貝爾獎發起人高舉當年其中一個獎盃。

2013年獲獎項目包括發現銀河能為屎殼郎引路，還有如何接上被嫉妒的妻子割下的陰莖。

2007年的「雞生蛋生雞」獎座。

---

基本概念：力學

力學是物理世界的重要範疇，接下來提到的四項實驗都與力學有關，而應用力學本身亦可以分為靜力學、 動力學、運動學。靜力學研究物體的平衡狀態；動力學研究物體的運動狀態和因素；運動學則把物體視為「剛體」，專門描述物體的運動，而不考慮作用力、質量、性質等，應用力學較常用作解決工程技術問題。

---

2021：街頭動力學→行路勿低頭

街道人來人往，為甚麼我們很少迎頭相撞？物理學家提出了「自我組織」（self-organization）， 解釋「行人自動跟隨相同方向人潮」的現象。但是，自從出現了智能手機，人人成為低頭族，打破了這項不明文規定。東京大學先端科學技術研究中心的村上久（Hisashi Murakami）博士邀請了五十四名大學生，分成左右兩組，各二十七人。兩邊的人分別戴上黃色和紅色的帽，以正常的走路速度朝另一邊前進，研究者以攝影自動追蹤系統，記錄和研究他們的行進速度、分布、轉彎角度等數據，改變不同變項，最後得出研究結果。

他發現只要路人隊伍的「領頭羊」滑手機，緊隨其後的路人便很容易「方寸大亂」，造成大擠塞的情況；相反，若是隊伍的中間或後面的路人滑手機，對行人路秩序產生的影響則少得多。

（圖一）B部分顯示不同情況下的實驗結果，如左上方的圖表，顯示行人隊伍前方的人滑手機，路上便會呈現一片紛亂的狀態，整條隊伍的行進速度都會變慢，形成人流的時間拉長至六秒。

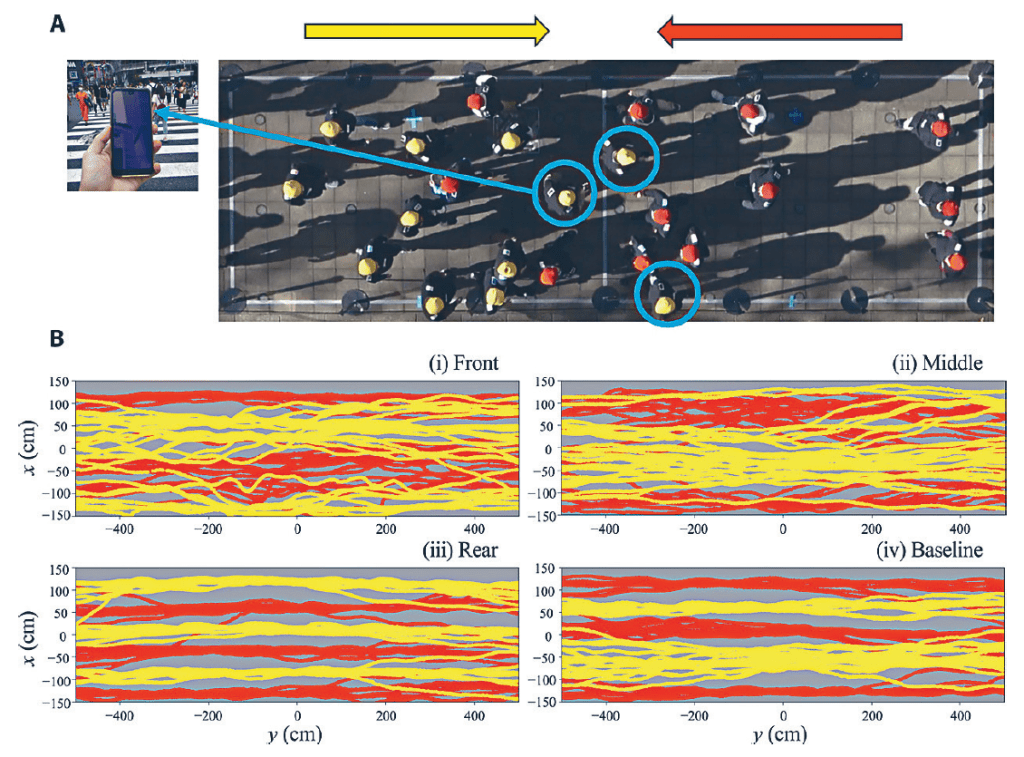
有興趣了解研究過程的同學點擊這裡閱讀完整論文。

2017：流體動力學→倒着捧咖啡

同學有沒有試過「倒瀉」飲品？ 如果有，便要學學二○一七年「搞笑諾貝爾獎」得主Han-Ji-Won，他還在韓國讀高中的時候，就以十五頁論文研究得出「最強」捧咖啡方法：「抓住杯口，向前看，倒着走。」

看來令人哭笑不得的研究題目，自然少不了實際的科學知識和嚴謹的研究方法。這名「無聊」的韓國高中生觀察一般人捧咖啡杯的情況，發現杯內液體的晃動可分成前後、左右、上下幾種模式，而不同模式之間晃動的頻率並不一致，當晃動疊合，杯內液體便會調皮地溢出；加上不同形狀的杯子亦會影響液體的晃動模式。

（圖二）（a）、（b）分別是馬克杯和紅酒杯以2Hz的頻率振動，可見紅酒杯中的液體表現得極不安分。 （c）、（d）以4Hz的頻率重複實驗，這一次，液體直接從馬克杯中跑出來，另一邊紅酒杯的液體反而不動如山。

（圖三）經過實驗和計算：在頻率為3.8Hz的時候，液體的振幅最大，最容易溢出杯子。

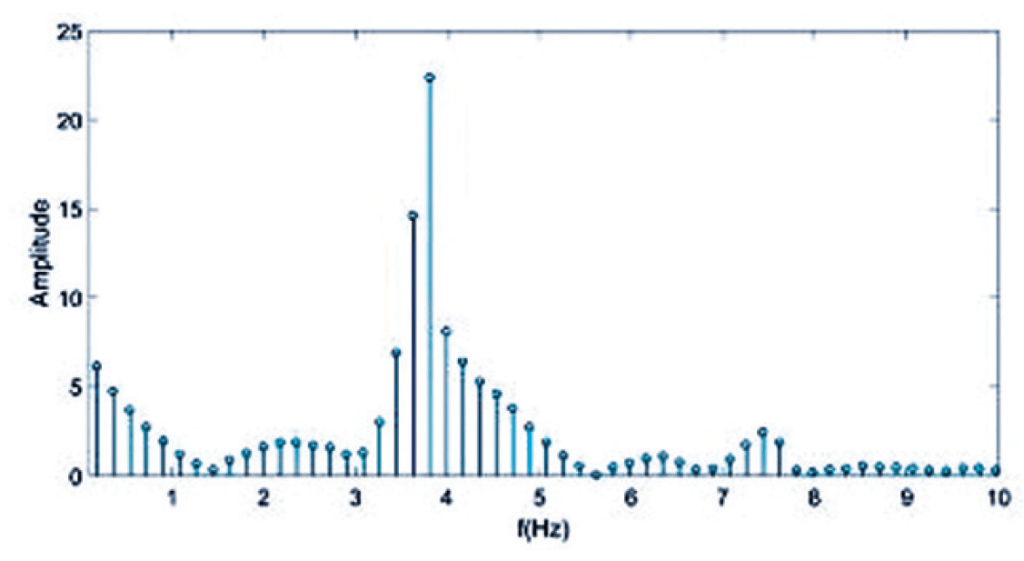
至此，我們已得出幾個影響液體溢出的變量，那麼要如何找出最不容易令液體溢出的方法呢？

手機APP記錄移動數據

原來這個實驗十分簡單，只要你有一部智能手機，下載能夠記錄手機移動數據的應用程式（Sensor Logger），打開程式後把手機蓋在杯子上，模擬不同的行走方法，程式會記錄手機前後、左右、上下的方位改變、速度，甚至磁場改變，分析這些數據，例如頻率和振幅，找出最理想的捧杯方式。

（圖四）從手機紀錄的數據可以得出拿杯子時的振動頻率，「拆解咖啡溢出背後的原理」。研究最後建議大家以五指抓住杯口，是防止咖啡溢出的最佳方法。

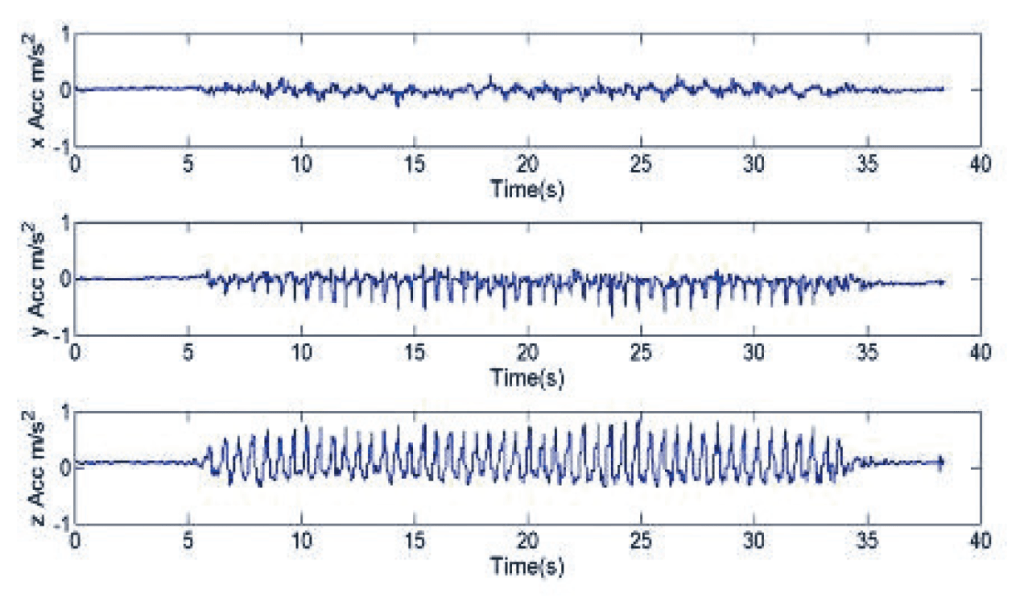
充滿好奇心的同學，不難想像在日常生活中，也可以利用這個應用程式來研究身邊大小事，例如「哪一條巴士綫路最適合睡覺」、「如何跑步最省力」等等，只要多觀察，科學實驗原來也可以很簡單。

Sensor Logger App

• iOS 下載連結
• Android下載連結

有興趣了解研究過程的同學點擊這裡閱讀完整論文。

2014：香蕉摩擦力→滑倒的真相

踩蕉皮滑倒的畫面常令人捧腹大笑，是電影中常見的橋段，不知道各位同學有沒有踩蕉皮的經驗呢？日本北里大學的研究團隊決定認真研究「香蕉皮有多滑」，找出蕉皮令人滑倒的真相，這項看似開玩笑的科學研究，奪得二○一四年「搞笑諾貝爾獎」。

日本北里大學學者馬淵清資（Kiyoshi Mabuchi）展示「香蕉皮有多滑」的研究成果。

這個「搞笑」的實驗用上可以測量正向力和橫向力的感知器，在感知器上放一塊地板，地板上放置黃皮朝上的香蕉皮，然後「不幸」的研究人員穿鞋子踩上去一滑，將結 果得出的橫向力除以正向力（μ =(fx2+fy2)0.5/fz），可得出蕉皮與地板之間的摩擦系數。多次測試後，研究團隊的得出蕉皮的摩擦系數是0.07。研究又引用其他科學文獻指出，對一般人的行路模式而言，腳踏在摩擦系數低於0.1的表面，滑倒機率大於百分之九十。

（圖五）研究報告〈Frictional Coefficient under Banana Skin〉中實驗裝置的示範圖。

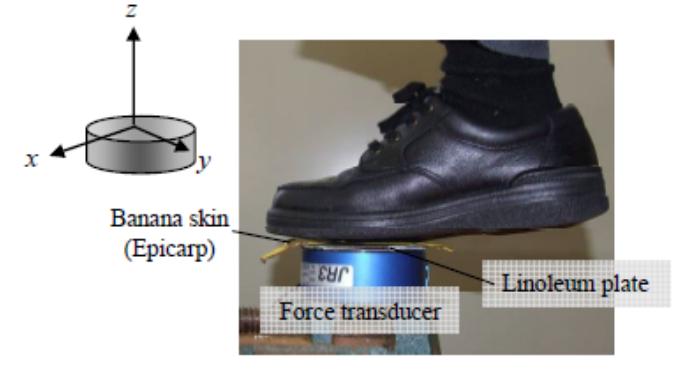
有興趣了解研究過程的同學點擊這裡閱讀完整論文。 

---

補充資料

摩擦系數（Friction）

摩擦系數是兩個物體表面之間，摩擦力與正向壓力的比值，受滑動面的性質、粗糙度、表面狀態影響，數值愈大，代表物件表面愈粗糙。下表是一 些常見物件之間的摩擦系數。

物件一	物件二	表面狀態	（靜）摩擦系數（μ）
冰	冰	清潔	0.1
木材	木材	乾燥	0.4
皮革	橡膠	乾燥	0.61
汽車胎	瀝青	乾燥	0.72

---

1996：牛油面着地→麵包力學圖

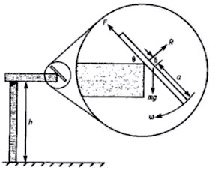
來自國外的都市傳聞，麵包總是以塗有牛油的一面着地 （Bread always falls on the buttered side down），最初來自詩人的諷刺，透露對日常中「微不幸」的無奈。英國物理學家羅伯特．馬修斯（Robert Matthews）是墨菲定律（Murphy's law）的研究學者，他非常嚴肅地面對這個問題，決定用科學方法去驗證這個都市傳聞，設計麵包墜地的力學圖（見圖六），數學計算牛油面向地板的概率，寫成論文〈掉落的吐司、墨菲法則和基本常數〉發表於《歐洲物理學期刊》，勇奪一九九六年的「搞笑諾貝爾獎」。

經過幾頁紙的數學計算，羅伯特的結論只是，「從早餐桌上掉下的吐司會以牛油的一面着地，是宇宙中必然會發生的。」但因為數學模型的限制，無法完全考慮現實的各種影響因素，羅伯特其後以實驗方式，統計一千次麵包掉在地板的結果，在9,821次有效掉落結果，其中6,101次以牛油一面落地，概率達到62%，超出常理50%的預測結果，某程度支持了這項都市傳聞。

（圖六）

有興趣了解研究過程的同學點擊這裡閱讀完整論文。  

---

補充資料

墨菲定律（Murphy's law）

墨菲定律指「有可能出錯的事總會出錯」，大多時候會從心理學的角度去解釋，但其實亦可以數學式表達：

設出錯的概率為E、重複做一件事的次數為n，那麼不出錯的概率可以1 - E（全部可能－出錯的可能＝不出錯的可能）表示，而連續n次不出錯的概率為（1 - E）^n。

試考慮一下，不能連續n次不出錯的概率（即在n次中，至少出錯1次的概率）便可得出數學式：

P（possibility）= 1 -（1 - E）^n

因為0<1 - E<1，所以當n愈大（重複次數愈多），（1 - E）^n愈接近0，即P愈接近1（「1」在概率上代表必然發生）。

結論是，只要重複做一件事情的次數足夠多，便一定會發生錯誤；也許各位同學下次做錯題目，可以用墨菲定律跟老師解釋是因為功課太多了。

---

文：盧家彥、星島中學學生報《S-FILE》編輯部；圖：網上圖片