奧妙的畢氏定理|星島教室
2024-12-19 11:40 
我們學習數學一定學習過直角三角形,當中有一個著名的理論——畢氏定理(Pythagorean theorem)。生活中我們不知不覺地應用這個理論。其實畢氏定理不僅是數學中的基礎理論,還在現代生活和技術中有許多實際應用,例如過馬路、走斜坡、走捷徑等,都經常運用畢氏定理。
何謂「畢氏定理」?
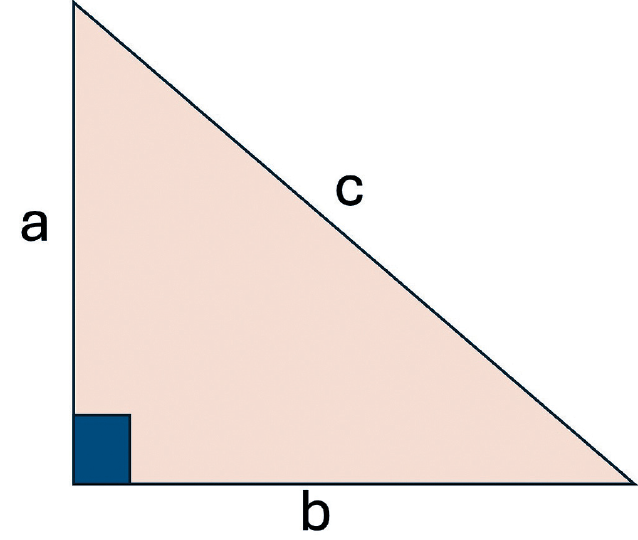
這個定理告訴我們,直角三角形中的兩條短邊的平方和等於長邊的平方。這條長邊叫做斜邊,也是直角對面的那條邊。
「畢氏定理」的公式是: a2+b2=c2
a和b是直角三角形的兩條邊
c是斜邊(最長的那條邊)
假設一個直角三角形,它的兩條邊長(a和b)分別是3米和4米。你可以用畢氏定理來計算斜邊的長度:32+42=c2,即是,9+16=c2,所以:25=c2,√25=c,5=c。因此,我們可用此方法找出斜邊的長度是5米。
生活解難
1. 最短路線

在一條繁忙的街道上,想由紅點走到紅色箭嘴。你可以先沿着橙色路線,連續過兩條斑馬線,亦可以直接沿着藍色路線走,這樣更快,更省時間。你可以用畢氏定理來計算這條最短的藍色路線的距離。
假設其中一條路線長40米,另一路線長30米,你想知道由紅點走到紅色箭嘴的最短距離,我們可以根據畢氏定理,計算藍色路線的長度:302+402=藍色路線2,√2500=藍色路線,藍色路線的長度是50米。換言之,如果我們走藍色路線的路程,比過兩條斑馬線(30+40=70)短。
2. 滑梯長度
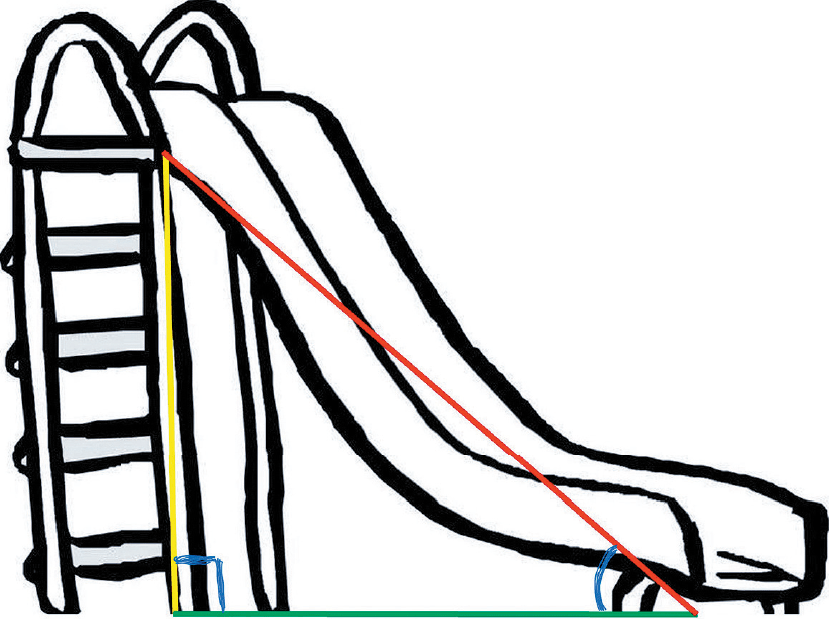
滑梯是我們經常玩的玩具,設計者常須計算滑梯的實際長度,以確保滑行的舒適性和安全性。這個長度可通過畢氏定理來計算,當我們已知滑梯的高度和水平距離時,滑梯長度就是這兩者形成的直角三角形的斜邊。
圖3是一個滑梯,黃色線是1米高,綠色線有1.5米長,黃色線和綠色線是互相垂直,因此可通過畢氏定理來計算紅色線滑梯的長度:12+1.52=滑梯長度2,即是√3.25=滑梯的長度,那麼滑梯的長度約1.8米。
另外,滑梯的長度和坡度會直接影響滑行的速度和感受。通過計算滑梯的實際長度,設計師便可確保滑梯的坡度不會過於陡峭,從而提供一個既安全又有趣的滑行體驗。假若坡度較平緩的滑梯,適合兒童使用,這樣,黃色線高度保持不變,而綠色水平線延長至3米,如此綠色水平線與紅色斜邊的角度會降低,而紅色線的長度可利用畢氏定理來計算:平緩滑梯長度=√(12+32)=√103.16米。換言之,如要坡度較低,較平緩的滑梯,需要水平長度和斜邊長度較長的滑梯。
3. 最短路徑
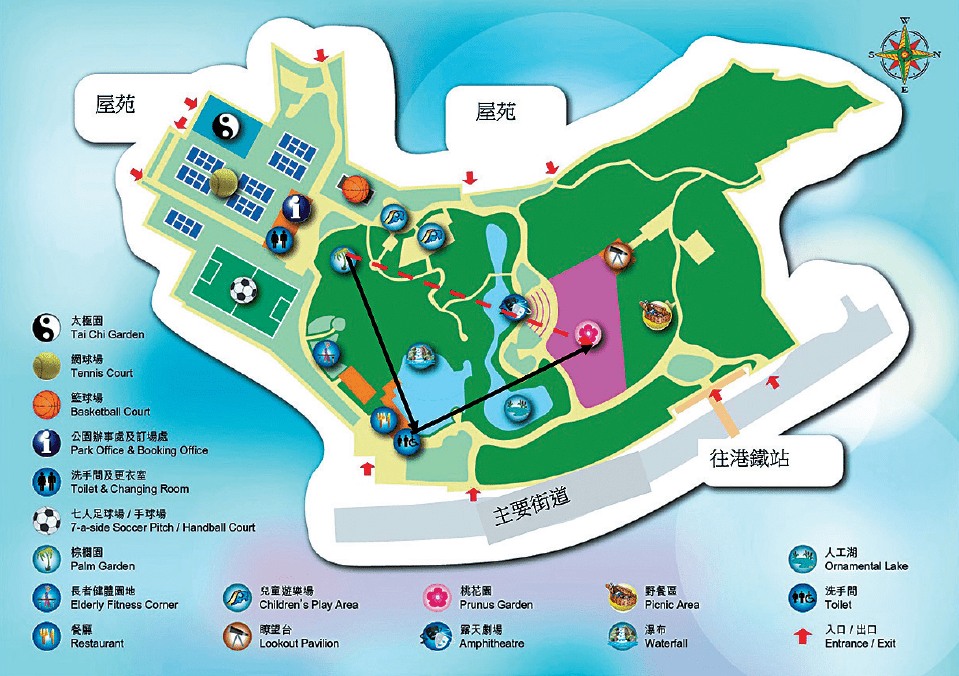
我們要走出一個面積大的地方,捷徑是最快又最省力的方法。如果你在公園的棕櫚園,想走到桃花園。你可以有兩個選擇︰先沿着黑色路線,經過餐廳和廁所,然後再經過第二條黑色路線,再到桃花園,這個方法不但浪費時間,又浪費力氣;但走紅色路線會更快。這個時候,你可以用畢氏定理來計算這條最短的紅色線路程。
假設公園的一邊是30米,另一邊是40米,你想知道走對角線的最短距離是多少。根據畢氏定理,我們可以計算出從棕櫚園到桃花園最近的距離:302+402=棕櫚園到桃花園最近的距離2,即是√2500=棕櫚園到桃花園最近的距離,因此從棕櫚園到桃花園最近的距離是50米。換言之,在一個直角三角形里,構成直角的兩條邊長長度相加一定是比斜邊長,所以斜邊是最短的。
GPS計算距離
GPS(全球定位系統)的運作原理中涉及大量數學計算,其中包括畢氏定理的應用。雖然GPS本身運用了更為複雜的數學(如三角測量和相對論效應),但在某些情況下,畢氏定理可用來解決GPS定位中的問題,特別是當我們處理平面距離或簡單的距離計算時。
畢氏定理在全球定位系統(GPS)中非常重要。GPS通常依賴於從多顆衛星發送的信號來確定某個物體或人的位置。每顆衛星會發送到達接收器的信號,GPS接收器可根據這些信號計算出兩個地方之間的距離。
當然,我們只考慮在地球上水平平面上的定位,就可以使用畢氏定理來進行簡化計算。當我們知道某個點的經緯度時,通過畢氏定理就可以計算兩點之間的直線距離。
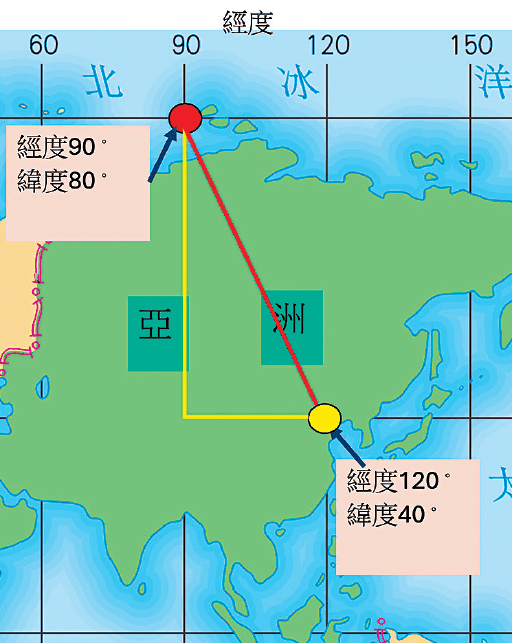
例如:假設GPS確定了兩個點的水平位置,該點是紅點(經度90度,緯度80度)與黃點(經度120度,緯度40度),即是垂直黃色線是緯度相減(80度-40度)=40單位,而水平黃色線是經度相減(120度-90度)=30單位。此時,我們可用畢氏定理來計算兩點之間的直線距離,即平面上最短距離。
根據畢氏定理:
兩點距離=√(402+302)=√2500=50單位
因此,紅點與黃點之間的直線距離為50單位。這種情況下,GPS接收器可知道自己在平面上的具體位置,並根據位置與其他點距離進行計算。
畢氏定理不僅僅是一個數學公式,它在日常生活中有許多應用。無論是計算斜台的長度、走最短的路,還是GPS上的應用,畢氏定理是一個非常有用的工具來計算平面或空間中的直線距離。無論是在導航、計算水平距離,還是高度差的問題中,畢氏定理都能提供簡單而有效解法。希望你能通過這些例子,學會在生活中應用畢氏定理。
小思考,大智慧
如果遇到非直角三角形的生活難題,我們可以應用哪些理論?
參考答案
我們可使用其他數學工具來解決,比如「正弦定理」和「餘弦定理」。這些定理都可以幫助我們處理非直角三角形中的邊長和角度計算,並且在很多實際應用中皆非常有用。
本欄逢周四刊登,由教育評議會邀請資深中小學老師、校長及大學講師撰稿,旨在為學生提供多元化的STEAM學習材料,引發學生探求知識的興趣,將學習融入生活,培養學生的世界觀、敏銳的觸覺、積極學習的態度。
文:中華基督教會蒙黃花沃紀念小學數學科主任 葉劍㷨、中華基督教會蒙黃花沃紀念小學老師周偉強博士
延伸閱讀:











最新回應